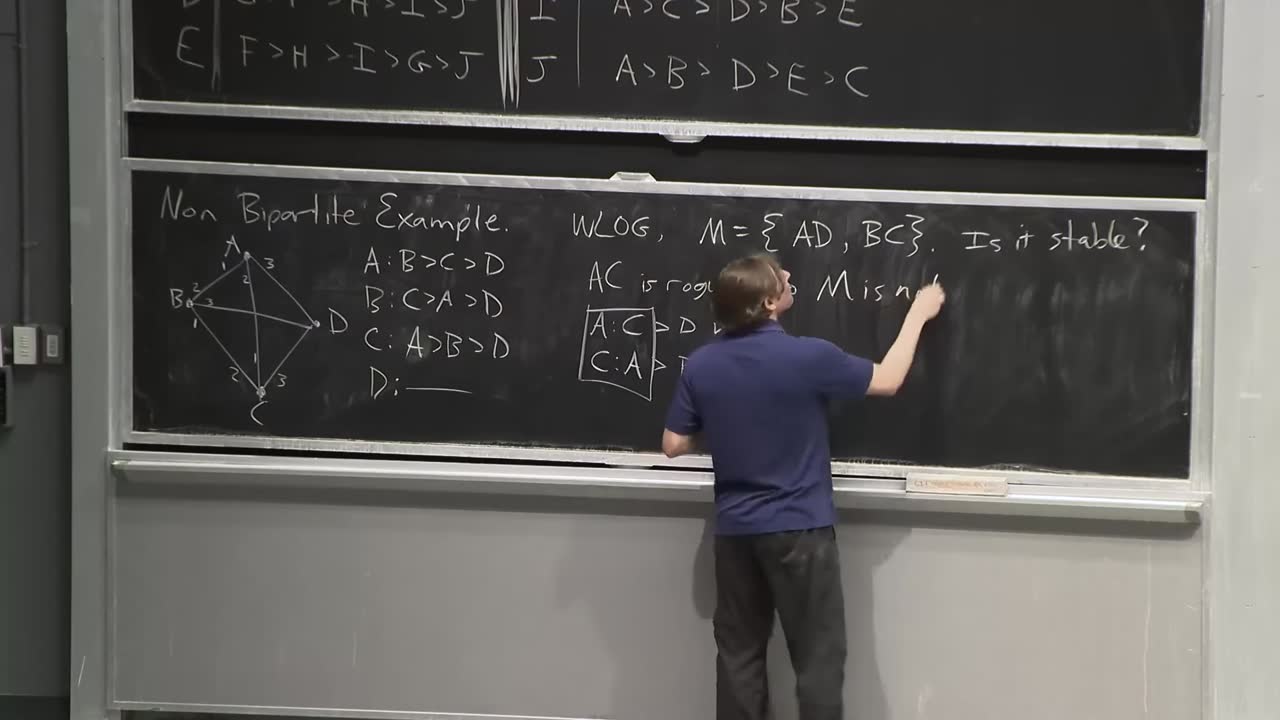Lecture 12: Matching
A matching in a graph G is a subgraph M of G in which every vertex has degree 1. In this lecture, we examine types of matching problems, such as maximum weight matching, stable matching, and matching in bipartite and non-bipartite graphs.
Source: Zachary Abel, Mathematics for Computer Science (MIT: OpenCourseWare). Licensed under CC BY-NC-SA 4.0.

Hypha Official
Watch what matters. Create what pays.
MIT 6.1200J: Mathematics for Computer Science
This course covers elementary discrete mathematics for science and engineering, with a focus on mathematical tools and proof techniques useful in computer science. Topics include logical notation, sets, relations, elementary graph theory, state machines and invariants, induction and proofs by contradiction, recurrences, asymptotic notation, elementary analysis of algorithms, elementary number theory and cryptography, permutations and combinations, counting tools, and discrete probability.
-
Lecture 1: Predicates, Sets, and Proofs1:18:46 Free
-
Lecture 2: Contradiction and Induction1:19:37 Free
-
Lecture 3: Casework and Strong Induction1:24:09 Free
-
Lecture 4: State Machines1:21:15 Free
-
Lecture 5: Sums1:22:20 Free
-
Lecture 6: Asymptotics1:18:25 Free
-
Lecture 7: Recurrences1:13:23 Free
-
Lecture 8: Divisibility1:18:59 Free
-
Lecture 9: Modular Arithmetic1:19:45 Free
-
Lecture 10: Cryptography1:21:08 Free
-
Lecture 11: Graphs and Coloring1:21:15 Free
-
Lecture 12: Matching1:21:43 Free
-
Lecture 13: Connectivity and Trees1:22:02 Free
-
Lecture 14: Digraphs and DAGs1:19:01 Free
-
Lecture 15: Relations and Counting1:18:46 Free
-
Lecture 16: Counting Techniques1:15:13 Free
-
Lecture 17: More Counting Techniques1:20:56 Free
-
Lecture 18: Probability1:07:58 Free
-
Lecture 19: Conditional Probability1:20:44 Free
-
Lecture 20: Independence1:22:02 Free
-
Lecture 21: Random Variables1:10:47 Free
-
Lecture 22: Expectation1:20:30 Free
-
Lecture 23: Expectation and Variance1:18:16 Free